这篇文章是 DeepLearning.ai - Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization Week 2 的课程笔记

指数加权平均

关键方程

${v}_{t}=\beta {v}_{t-1}+(1-\beta ){\theta }_{t}$

${\theta }_{t}$为当前计算数据，${v}_{t-1}$为前一次计算的结果

偏差修正

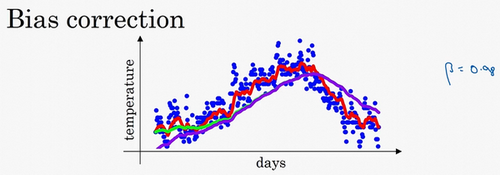
${v}_{0}$初始化为一个较小的数，导致对下标小的项的估测偏差较大。可以在预测初期不用${v}_{t}$，而是用$\frac{v_{t}}{1- \beta^{t}}$。随着t的增加，分母会逐渐趋向于1，修正偏差将基本没什么作用；但在t较小的时候，能够较好地修正。

动量梯度下降

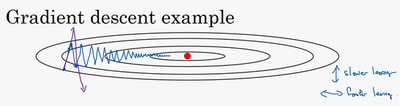
无论使用full batch还是mini batch，梯度下降的效果大致如上图所示。我们不停地更新w和b的值，让函数移动到红色点的位置，获得全局最优解。但在这个过程中，在纵轴上下波动，而在横轴会逐渐向最优解方向移动。我们希望的是，在纵轴上的波动能越小越好，而在横轴上的前进距离每次越大越好。在纵轴上的波动越大，会导致横轴上的前进距离也越小。我们可以通过增加迭代次数或者调大学习率来加快到最优解的速度，但增加迭代次数会增加训练时间，而增大学习率会导致摆动增大，误差增大。这里我们可以用到动量梯度下降法。

在每次迭代中，确切来说在第$t$次迭代的过程中，会计算微分$dW$，$db$。这样就可以减小梯度下降的幅度。

$v_{dW}= \beta v_{dW} + \left( 1 - \beta \right)dW$
$v_{db}$，$v_{db} = \beta v_{db} + ( 1 - \beta){db}$
$W:= W -av_{dW}$
$b:= b - a v_{db}$

这里将之前的$dW$和$db$都联系起来，不再是每一次梯度都是独立的情况。此时的梯度不再只是现在的数据的梯度，而是有一定权重的之前的梯度。

如果把梯度下降法想象成一个小球从山坡到山谷的过程，那么前面几篇文章的小球是这样移动的：从A点开始，计算当前A点的坡度，沿着坡度最大的方向走一段路，停下到B。在B点再看一看周围坡度最大的地方，沿着这个坡度方向走一段路，再停下。确切的来说，这并不像一个球，更像是一个正在下山的盲人，每走一步都要停下来，用拐杖来来探探四周的路，再走一步停下来，周而复始，直到走到山谷。而一个真正的小球要比这聪明多了，从A点滚动到B点的时候，小球带有一定的初速度，在当前初速度下继续加速下降，小球会越滚越快，更快的奔向谷底。momentum 动量法就是模拟这一过程来加速神经网络的优化的。

这里有两个超参数，学习率$\alpha$和$\beta$，$\beta$最常用的值为0.9。这里一般不进行偏差修正，因为10次迭代之后，移动平均已经过了初始阶段实际中，在使用梯度下降法或动量梯度下降法时，人们不会受到偏差修正的困扰。当然v_初始值是0，要注意到这是和$dW$拥有相同维数的零矩阵，也就是跟$W$拥有相同的维数，$v_{db}$的初始值也是向量零，所以和$db$拥有相同的维数，也就是和$b$是同一维数。

RMSprop (Root Mean Square Prop)

关键方程

$S_{dW}= \beta S_{dW} + (1 -\beta) {dW}^{2}$
$S_{db}= \beta S_{db} + (1 - \beta){db}^{2}$
$W:= W -\alpha\frac{dW}{\sqrt{S_{dW}}}$
$b:=b -\alpha\frac{db}{\sqrt{S_{db}}}$

原理

• $W$的在横轴上变化变化率很小，所以$dW$的值十分小，所以$S_{dw}$也小，而$b$在纵轴上波动很大，所以斜率在b方向上特别大。所以这些微分中，$db$较大，$dw$较小。这样$W$除数是一个较小的数，总体来说，$W$的变化很大。而$b$的除数是一个较大的数，这样$b$的更新就会被减缓。纵向的变化相对平缓。
• 这里的$W$和$b$标记只是为了方便展示，在实际中这是一个高维的空间，很有可能垂直方向上是$W_{1}$,$W_{2}$,$W_{5}$…的合集而水平方向上是$W_{3}$,$W_{4}$,$W_{6}$…的合集。
• 实际使用中，为了防止分母为0，公式建议为

$W:= W -\alpha\frac{dW}{\sqrt{S_{dW}+\epsilon}}$
$b:=b -\alpha\frac{db}{\sqrt{S_{db}+\epsilon}}$

Adam

基本原理是将Momentum和RMSprop结合在一起。

初始化

$v_{dW} = 0$
$S_{dW} =0$
$v_{db} = 0$
$S_{db} =0$

计算Momentum指数加权平均数

$v_{dW}= \beta_{1}v_{dW} + ( 1 - \beta_{1})dW$
$v_{db}= \beta_{1}v_{db} + ( 1 -\beta_{1} ){db}$

计算RMSprop更新

$S_{dW}=\beta_{2}S_{dW} + ( 1 - \beta_{2}){(dW)}^{2}$
$S_{db} =\beta_{2}S_{db} + \left( 1 - \beta_{2} \right){(db)}^{2}$

相当于Momentum更新了超参数$\beta_{1}$，RMSprop更新了超参数$\beta_{2}$。

修正偏差

$v_{dW}^{\text{corrected}}= \frac{v_{dW}}{1 - \beta_{1}^{t}}$
$v_{db}^{\text{corrected}} =\frac{v_{db}}{1 -\beta_{1}^{t}}$
$S_{dW}^{\text{corrected}} =\frac{S_{dW}}{1 - \beta_{2}^{t}}$
$S_{db}^{\text{corrected}} =\frac{S_{db}}{1 - \beta_{2}^{t}}$

更新权重

$W:= W - \frac{a v_{dW}^{\text{corrected}}}{\sqrt{S_{dW}^{\text{corrected}}} +\varepsilon}$
$b:=b - \frac{\alpha v_{\text{db}}^{\text{corrected}}}{\sqrt{S_{\text{db}}^{\text{corrected}}} +\varepsilon}$

所以Adam算法结合了Momentum和RMSprop梯度下降法，并且是一种极其常用的学习算法，被证明能有效适用于不同神经网络，适用于广泛的结构。

超参数

本算法中有很多超参数，超参数学习率$a$很重要，也经常需要调试，可以尝试一系列值，然后看哪个有效。$\beta_{1}$常用的缺省值为0.9，这是dW的移动平均数，也就是$dW$的加权平均数，这是Momentum涉及的项。至于超参数$\beta_{2}$，Adam论文作者，也就是Adam算法的发明者，推荐使用0.999，这是在计算${(dW)}^{2}$以及${(db)}^{2}$的移动加权平均值，关于$\varepsilon$的选择没那么重要，Adam论文的作者建议$\varepsilon$为$10^{-8}$，但一般并不需要设置它，因为它并不会影响算法表现。但是在使用Adam的时候，人们往往使用缺省值即可，$\beta_{1}$，$\beta_{2}$和$\varepsilon$都是如此。

SGD

Batch Gradient Descent

在每一轮的训练过程中，Batch Gradient Descent算法用整个训练集的数据计算cost function的梯度，并用该梯度对模型参数进行更新

优点

• cost function若为凸函数，能够保证收敛到全局最优值；若为非凸函数，能够收敛到局部最优值

缺点

• 由于每轮迭代都需要在整个数据集上计算一次，所以批量梯度下降可能非常慢
• 训练数较多时，需要较大内存
• 批量梯度下降不允许在线更新模型，例如新增实例

Stochastic Gradient Descent

和批梯度下降算法相反，Stochastic gradient descent 算法每读入一个数据，便立刻计算cost function的梯度来更新参数

优点

• 算法收敛速度快(在Batch Gradient Descent算法中, 每轮会计算很多相似样本的梯度, 这部分是冗余的)
• 可以在线更新
• 有几率跳出一个比较差的局部最优而收敛到一个更好的局部最优甚至是全局最优

缺点

• 容易收敛到局部最优，并且容易被困在鞍点

Mini-batch Gradient Descent

mini-batch Gradient Descent的方法是在上述两个方法中取折衷, 每次从所有训练数据中取一个子集（mini-batch） 用于计算梯度

主要挑战

• 选择适当的学习率$\alpha$较为困难。太小的学习率会导致收敛缓慢，而学习速度太块会造成较大波动，妨碍收敛。
• 目前可采用的方法是在训练过程中调整学习率大小，例如模拟退火算法：预先定义一个迭代次数m，每执行完m次训练便减小学习率，或者当cost function的值低于一个阈值时减小学习率。然而迭代次数和阈值必须事先定义，因此无法适应数据集的特点。
• 上述方法中, 每个参数的 learning rate 都是相同的，这种做法是不合理的：如果训练数据是稀疏的，并且不同特征的出现频率差异较大，那么比较合理的做法是对于出现频率低的特征设置较大的学习速率，对于出现频率较大的特征数据设置较小的学习速率。
• 近期的的研究表明，深层神经网络之所以比较难训练，并不是因为容易进入local minimum。相反，由于网络结构非常复杂，在绝大多数情况下即使是 local minimum 也可以得到非常好的结果。而之所以难训练是因为学习过程容易陷入到马鞍面中，即在坡面上，一部分点是上升的，一部分点是下降的。而这种情况比较容易出现在平坦区域，在这种区域中，所有方向的梯度值都几乎是 0。

参考资料

1. An overview of gradient descent optimization algorithms
2. Optimization Algorithms优化算法
3. 深度学习优化函数详解（4）-- momentum 动量法