这篇文章是 DeepLearning.ai - Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization Week 3 的课程笔记

Hyperparameter Tuning

超参数重要性排序：

• ${\alpha}$
• 动量${\beta}$、#hidden_units、mini-batch大小
• 层数、学习率衰减

Adam中的${\beta_1}$，${\beta_2}$，${\epsilon}$一般不需要调整

寻找最优超参数的尺度

• Alpha的取样：使用对数尺度而不是线性尺度，因为${\alpha}$通常在0.0001, 0.001, 0.01, 0.1中取样
  • 要基于对数尺度取样，首先取得下限值，取其对数得到a，取得上限值，取其对数得到b，然后在对数尺度上在${10^a}$ ~ ${10^b}$ 范围内取样，r在[a, b]范围内取样，alpha就在${10^r} 的范围内
• ${\beta}$的取样：${\beta}$通常的选择范围是0.9, 0.99, 0.999, … 0.999999
  • 1-${\beta}$ = 0.1, 0.01, 0.001, …, 0.000001
  • r在[-3, -1]范围内

组织超参数搜索过程

• Babysit one model (Panda)
  • 没有足够的计算资源
  • 定时调整超参数
• Train many models in parallel (Caviar)
  • 同时训练不同超参数设置的模型，选最好的那个

Batch Normalization

在逻辑回归中，对输入做归一化处理能加快回归速度。对于更复杂的网络，除了输入外，能否归一化每层的参数来加快训练速度？

隐藏层归一化后均值和方差不一定要满足0和1（因为需要一些非线性特征），可通过$\tilde{z}^{(i)}= \gamma z_\text{norm}^{(i)} +\beta$ 构造特定均值和方差的隐藏层。这里的${\gamma}$和${\beta}$ 是可训练的（使用梯度下降、Momentum、Adam等）。

如果你没有应用Batch归一化，你会把输入X拟合到第一隐藏层，然后首先计算z1，这是由w1和b1两个参数控制的。接着，通常而言，你会把z1拟合到激活函数以计算a1。但Batch归一化的做法是将z1值进行Batch归一化，简称BN，此过程将由${\beta_1}$和${\gamma_1}$两参数控制，这一操作会给你一个新的规范化的z1值，然后将其输入激活函数中得到a1。

• 从神经网络后层之一的角度而言，前层不会左右移动的那么多，无论千前层参数如何变化，到后一层都会被同样的均值和方差所限制，所以，这会使得后层的学习工作变得更容易些。
• Batch归一化减少了输入值改变的问题，它的确使这些值变得更稳定，神经网络的之后层就会有更坚实的基础。即使使输入分布改变了一些，它会改变得更少。它做的是当前层保持学习，当改变时，迫使后层适应的程度减小了，你可以这样想，它减弱了前层参数的作用与后层参数的作用之间的联系，它使得网络每层都可以自己学习，稍稍独立于其它层，这有助于加速整个网络的学习。
• BN的一个副作用是能带来正则化效果，但不建议使用它来进行正则化，而是用它来加速训练。

Softmax回归

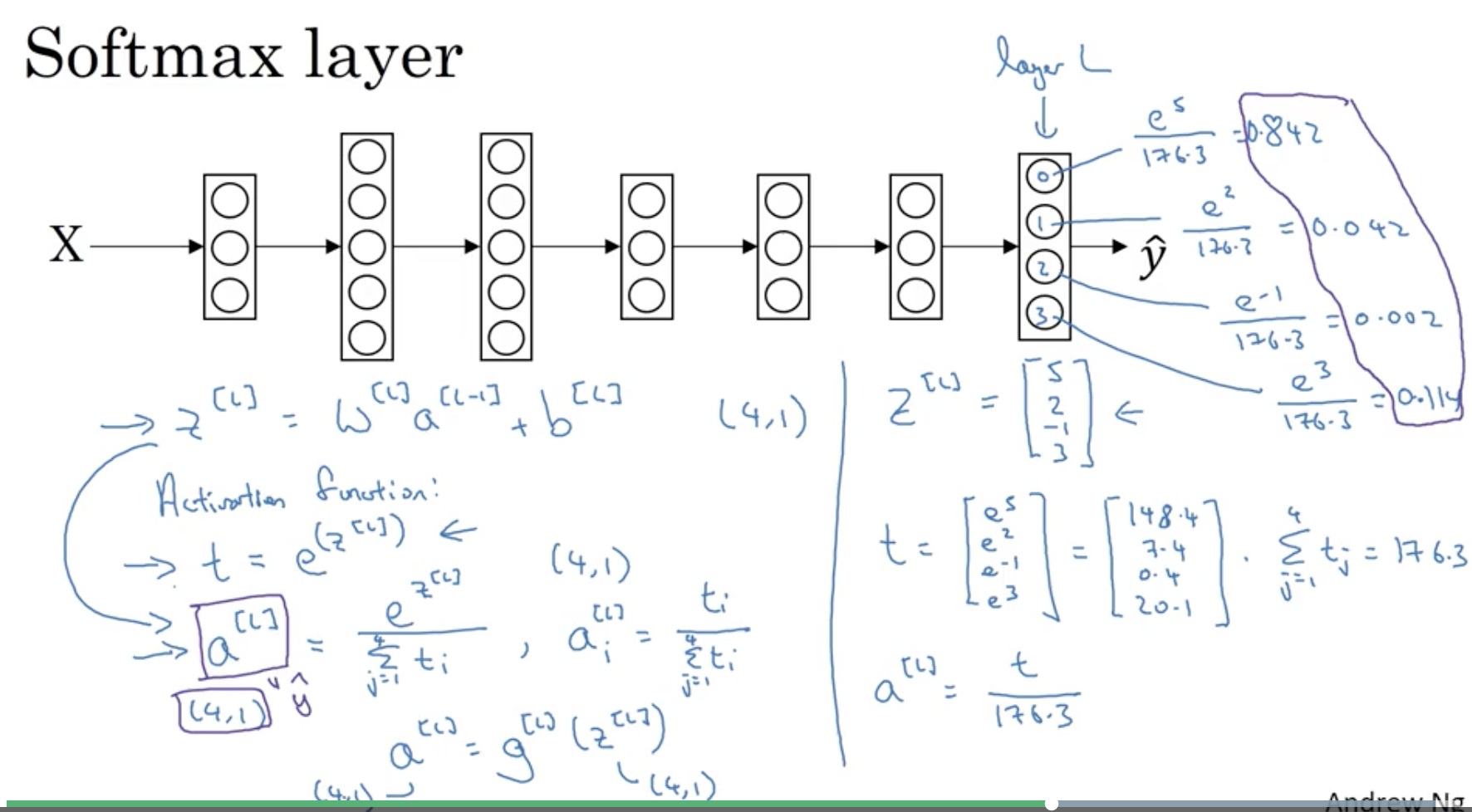
将Logistic回归推广为多分类

Loss Function

单个训练集

$L(\hat y,y ) = - \sum_{j = 1}^{4}y_{j}log\hat y_{j}$
希望损失函数越小，就希望$\hat y_{j}$越大，与$\hat y$中每一项代表概率是一致的。

整个训练集

$J( w^{[1]},b^{[1]},\ldots\ldots) = \frac{1}{m}\sum_{i = 1}^{m}{L( \hat y^{(i)},y^{(i)})}$
使用梯度下降